Archives

Chiral Molecule Scattering Experiments

Optical Activity

Optical Rotation

Chiral enantiomers of a molecule have identical physical properties - melting point, vapor pressure, etc. - with one exception: they scatter polarized light differently. For example, if linearly polarized light passes through a solution of chiral molecules (all of the same enantiomer), the plane of polarization will rotate. Most importantly, the two enantiomers of a molecule will rotate the plane of polarization in opposite directions. This phenomenon is called optical rotation.

This rotation is a result of circular birefringence: linearly polarized light can be decomposed into left- and right-circular polarization states, and optical rotation can be explained by attributing to the chiral molecules unequal real indices of refraction for circular waves of opposite rotational sense. The two waves thus acquire a relative phase shift that yields a net rotation of the original linear polarization. Here is a schematic of optical rotation: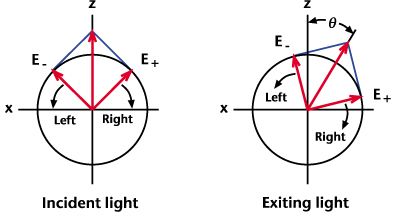



The degree of optical rotation is given by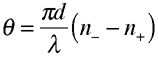



where d is the thickness of the molecular sample, λ is the light's wavelength, and n-(+) is the real index of refraction for left (right) circular light.

The nomenclature of chiral molecules incorporates optical rotation properties by adding (+) or (-) to the name of a compound. The (+) symbol refers to a dextrorotatory molecule. Such molecules rotate linearly polarized light to the right (clockwise) when viewed in the direction of light propagation. Molecules labeled with (-) are laevorotatory and rotate the polarization to the left (counterclockwise). Sometimes the letters D and L are used for these respective cases instead of (+) and (-).

It is important to note that the (+/-) notation does not necessarily correspond to the (R/S) notation mentioned previously. Some right-handed molecules (R) rotate light to the left (-), and vice versa, so that molecular nomenclature is not consistent in matching (+) with R or (-) with S. Here are some examples in which the notation schemes are combined and inconsistent:
R(-)-3,5-Dinitro-N-(1-phenylethyl)benzamide

R(+)-1,1'-Bi(2-naphthol)

S(-)-2-(Phenylaminocarbonyloxy)propionic acid

S(+)-1-(9-Anthryl)-2,2,2-trifluoroethanol


 The (+/-) notation is an outdated, ambiguous, and sometimes incorrect scheme of identifying configurations at a chiral center, but it does reveal information about the important physical property of optical activity.
For a recent development in determining the relationship between the 3-D structures of molecules and optical rotation, click here.


In addition to introducing optical rotation, chiral molecules can also cause unequal attenuation of left- and right-circularly polarized light because their indices of refraction are generally complex quantities. The imaginary component of the refractive index brings about exponential amplitude decay of circular light and has the overall effect of changing the light's ellipticity. This phenomenon is called circular dichroism.

The resulting elipticity (usually called Ψ) can be defined much like the rotation angle above: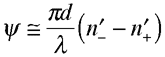

Here, n'-(+) are imaginary indices of refraction for circular light.

Below is an example schematic diagram of circular dichroism. Linearly polarized light shines on a chiral target and emerges elliptically polarized. The conversion from linear to elliptical light can be explained by decomposing the linear polarization into equal parts of left and right circular states. The two circular states are absorbed by the chiral sample at different rates and emerge with unequal amplitudes. Convoluting these opposite circular states of unequal amplitude gives an elliptical polarization state.



The attenuation of the circular electric field amplitudes can be written as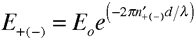


Click here for a more detailed tutorial of circular dichroism spectroscopy.

Optical rotation and circular dichroism are two of the more prominent phenomena involving chiral materials and polarized light, and here we refer to them both generally as optical activity. When linearly polarized light passes through a solution of chiral molecules, the overall effect is to produce elliptically polarized light (with ellipticity Ψ) rotated to an angle θ.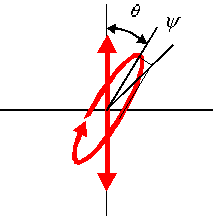

Archived: January 2020