Archives
Chiral Molecule Scattering Experiments
|
As mentioned previously, beams of electrons can be chiral (polarized) in a manner similar to photon beams. In fact, the mathematical description for electron polarization is exactly the same as that for photons. Why? Because both electron and photon polarization can be described in terms of a two-state spin function. 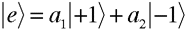
where What about electrons? Since electrons are spin-1/2 particles with ms=+/- 1/2 relative to a quantization axis, we can write the familiar spin state 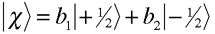
Then, by virtue of the similar forms of photonic and electronic spin states, we can write a more general expression for particles described by two-state spin functions: 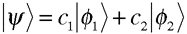
From this point, the polarization description of photon and electron beams can be described in terms of either density matrices or polarization (Stokes) vectors that are based on the function
Because of this close analogy between polarized photons and electrons, we can conjecture, as Peter Farago did in 1980, that electrons might experience polarization-dependent scattering from chiral molecules just as photons do. In other words: Before answering that question, let's first state exactly what electron optical activity is. As in the photon case, electron optical activity should comprise at least two prominent phenomena: electron optical rotation and electron circular dichroism. Recall that optical rotation involves the rotation of the plane of linearly polarized light as it passes through a chiral medium. Also recall that the electron version of linear polarization is transversepolarization (see the picture of photon and electron polarization analogies above). By analogy, then, electron optical rotation should involve the rotation of transverse electron polarization around the beam axis as the electrons pass through a chiral target. 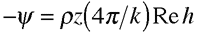
When scattering electrons off chiral molecules, the target is in the gas phase rather than in solution. Here, In the case of electron circular dichroism, a longitudinally polarized electron beam is attenuated according to its handedness, just as in optical circular dichroism. In this case, the attenuation of the beam is given by 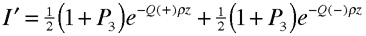
where P3 is the degree of electron longitudinal polarization, and Q (+/-) is the cross section for an individual scattering event (the signs +/- refer to molecular handedness). According to the optical theorem, the cross section is 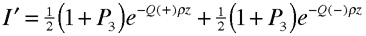
Here, f is the direct scattering amplitude. But the important feature of the cross section is that it is proportional to the imaginary component of the chiral scattering amplitude h, just as optical circular dichroism depends on the imaginary indices of refraction of the chiral target. |
||||
|
Archived: January 2020 |

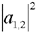 give the relative probabilities for an individual photon to pass through an analyzer which transmits only photons in the respective helicity eigenstates
give the relative probabilities for an individual photon to pass through an analyzer which transmits only photons in the respective helicity eigenstates 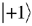 and
and 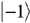 (right- and left-handed states).
(right- and left-handed states).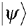 . The two formalisms are equivalent.
. The two formalisms are equivalent. is the density of that gas, z is the length of the target cell, k is the wave vector of the beam, and h is the chiral scattering amplitude. The chiral scattering amplitude depends on the geometry of the target molecules, and h has opposite signs for the two enantiomers of the molecules.
is the density of that gas, z is the length of the target cell, k is the wave vector of the beam, and h is the chiral scattering amplitude. The chiral scattering amplitude depends on the geometry of the target molecules, and h has opposite signs for the two enantiomers of the molecules.
