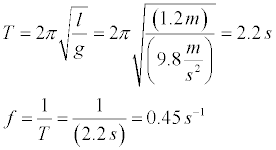

This recitation will focus on applications of simple harmonic motion involving springs and pendulums. Please experiment with the Physlet simulations below and complete the required calculations on your worksheet.
The physlet above allows you to watch a pendulum swinging back and forth with amplitudes up to 10°. This is the largest amplitude for which the pendulum obeys simple harmonic motion (where sinθ is no longer approximately equal to θ). You may use the pause button to stop the animation and the step buttons to move through the animation frame by frame. You can click anywere on the grid and read out the x and y values (assume units are in meters) of the cursor location. Click Simulate! below to begin the animation.
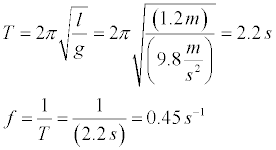

The animation above displays the motion of a mass oscillating on a horizontal spring.
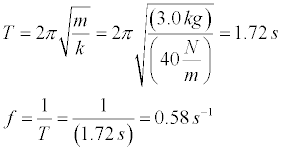
Since the kinetic energy at the release point is zero and the potential energy at the equilibrium position is zero, the conservation of energy can be stated simply as the potential energy at the release point must be equal to the kinetic energy at the equilibrium point. This relation can then be used to solve for the (maximum) velocity at the equilibrium point.
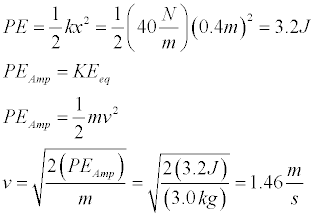
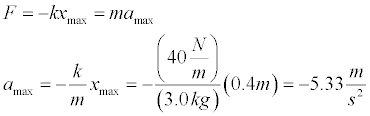
The starship Enterprise discovers a new planet. Captain Archer and Ensign Meriweather travel down to the planet in a shuttlepod. Since T'pol's sensors are presently useless due to ionization in the planet's upper atmosphere, they are forced to use primitive methods to learn about the planet. Ensign Meriweather sets up the pendulum shown above to measure the planet's acceleration due to gravity. The pendulum bob has a mass of 2.8 kg.