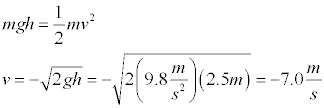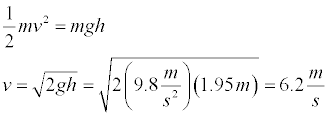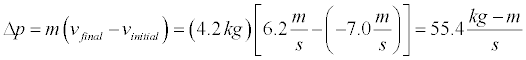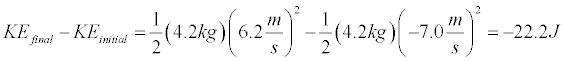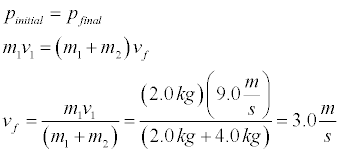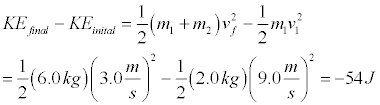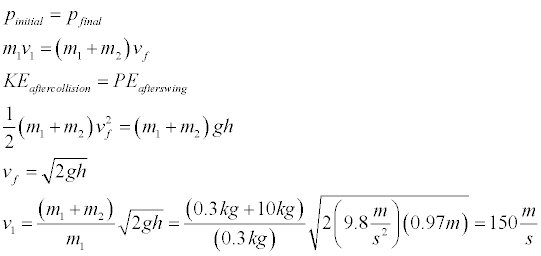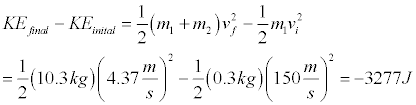Physics 151: Computerized Recitation #8

Conservation of Momentum

This recitation will focus on applications of the conservation of momentum and in some cases the conservation of energy will be involved as well. Please experiment with the Physlet simulations below and complete the required calculations on your worksheet.

Simulation 1: Change in Momentum

The physlet above allows you to watch a 4.2 kg basketball bounce off of the ground. The height (of the bottom of the ball) above the ground may be selected. You may use the pause button to stop the animation and the step buttons to move through the animation frame by frame. You can click anywere on the grid and read out the x and y values (assume units are in meters) of the cursor location. The change in momentum of the ball and the mechanical energy lost during the collision are calculated. This physlet is not precise and rounding errors are to be expected. Click Simulate! below to begin the animation.

Suggestions for Exploration

• Setup the simulation so that the basketball is dropped from a height of 2.5 m. We determine the velocity with which the ball will hit the ground by applying conservation of energy with the zero level potential at the ground. Note that since the y coordinate axis is pointed upwards, the ball has a negative velocity when falling.


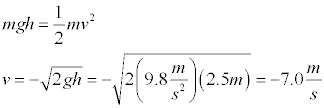
We don't expect that mechanical energy will be conserved since the ball is deformed as it hits the ground and some mechanical energy is transformed into thermal energy. We can figure out how much energy is "lost" by determining how much energy the ball has after the collision. To determine the velocity of the ball immediately after the impact with the ground, not that the ball rises to a height of 1.85 m above the ground and apply conservation of energy. Even though mechanical energy is not conserved during the collision, it is once again applicable after the collision.



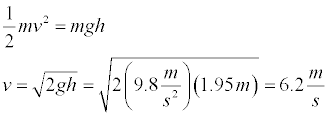
We can now evaluate the change in momentum that occurs during the bounce keeping in mind that momentum is a vector.



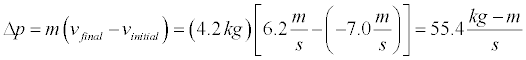
We can also evaluate the energy lost during the collision.


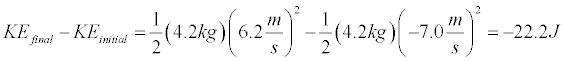
• Experiment with other values of the input parameters.
• Worksheet: Determine the value of the unknown height from the change in momentum and the kinetic energy lost.

Simulation 2: Inelastic Collision

The simulation above allows you to view the collision between two "mushy" balls - one moving and one stationary. The two balls then move off together. The final velocity and the mechanical energy lost during the collision are given as outputs.

Suggestions for Exploration

• Setup the simulation so that the mass of the first ball is 2.0 kg, its velocity is 9.0 m/s, and the mass of the second ball is 4.0 kg. We can use conservation of momentum to determine the velocity after the collision.


We can also calculate the mechanical energy converted into other forms during the collision.


• Experiment with other values of the input parameters.
• Worksheet: Determine the value of the unknown variables.

Simulation 3: Ballistic Pendulum

The physlet above simulates a ballistic pendulum. It is an apparatus commonly used to measure the velocity of bullets throught application of both the conservation for momemtun and the conservation of energy. Thus, although this simulation allows you to specify the velocity of the bullet, that is typically the unknown you are trying to determine with the ballistic pendulum.

• Setup the simulation so that the mass of the bullet m₁= 0.30 kg, its velocity is v₁150 m/s, and the mass of the wood block is 10.0 kg. We can use conservation of momentum to determine the velocity after the collision.


We can also calculate the mechanical energy converted into other forms during the collision.


• Experiment with other values of the input parameters.
• Worksheet: Determine the value of the unknown variables?