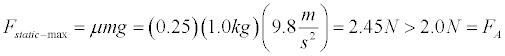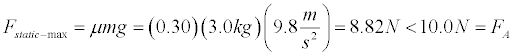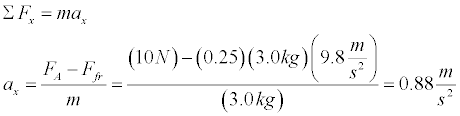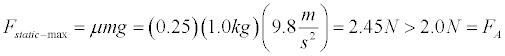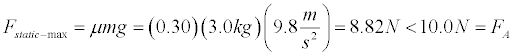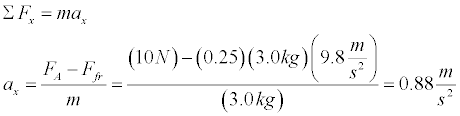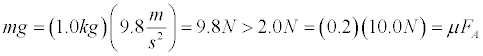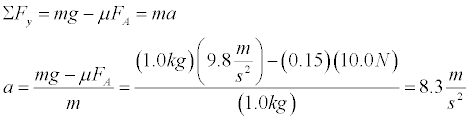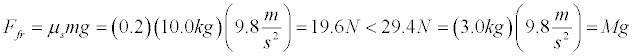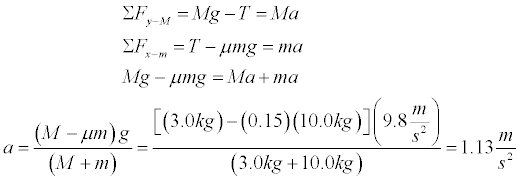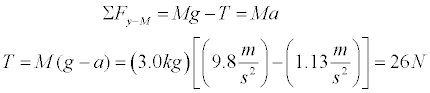Physics 151: Computerized Recitation #5

Forces II (Applications of Newton's Second Law with Friction)

This recitation will focus on applications of Newton's Second Law where friction is present. Please experiment with the Physlet simulations below and complete the required calculations on your worksheet.

Simulation 1: A Mass Being Pushed across a Horizontal Flat Surface with Friction

The physlet above allows you to watch a force acting a box across sitting on horizontal surface where friction is present. You may select the coefficient of static friction and the coefficient of kinetic friction is programmed to be 0.05 less. You may use the pause button to stop the animation and the step buttons to move through the animation frame by frame. You can click anywere on the grid and read out the x and y values (assume units are in meters) of the cursor location. Click Simulate! below to begin the animation.

Suggestions for Exploration

• Setup the simulation for an applied force of 2.0 N, mass = 1.0 kg, m_s= 0.25, and m_k= 0.20. Draw a free body diagram for the block. We need to compare the value of the applied force to the maximum value of static friction to determine whether acceleration will occur.


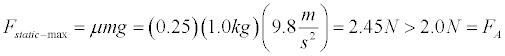
Thus, the acceleration is zero and the force of static friction is equal to the applied force.

• Setup the simulation for an applied force of 10.0 N, mass = 2.0 kg, m_s= 0.30, and m_k= 0.25. We agian need to compare the value of the applied force to the maximum value of static friction to determine whether acceleration will occur.


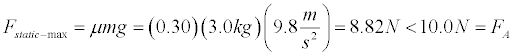
Thus, the mass will move and kinetic friction will be present. The normal force is simply equal to the weight of the mass in this situation.


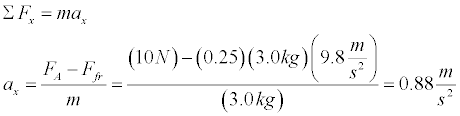
• Experiment with several other values of the input parameters and try to predict the acceleration and the frictional force.
• Worksheet: Determine the values of the unknown variables on your worksheet.

Simulation 2: Book Being Pushed Against the Wall

The physlet above simulates pressing a book against a rough wall. You can control the applied force, the mass of the book, and the coefficients of friction.

Suggestions for Exploration

• Run the simulation for the initial values of F_A = 10.0 N, mass = 1.0 kg, m_s= 0.20, and m_s= 0.15. Draw a free body diagram for the book. We need to compare the weight of the book to the maximum value of static friction to determine whether acceleration will occur.


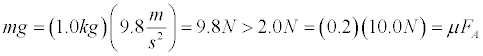
Thus, the acceleration will be non-zero since friction is insufficient to support the weight of the book. We now calculate the acceleration in the y direction (down-positive) using the coeficient of kinetic friction.


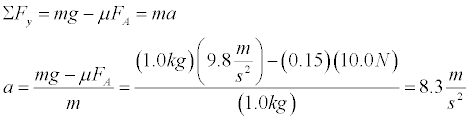
• Experiment with several other values of the input parameters and try to predict the acceleration and the frictional force.
• Worksheet: Determine the values of the unknown variables on your worksheet.

Simulation 3: Horizontal Atwood's Machine

The physlet above allows you to watch two masses connected by a massless rope strong over a massless pulley. One mass moves vertically and pulls the other horizontally. This is commonly referred to as a horizontal Atwood's Machine. Click Simulate! below to begin the animation.

Suggestions for Exploration

• Construct free body diagrams for the two masses. Again note that the masses will not move when the force of static friction of the horizontal mass is greater than the weight of the vertical mass. Let's work with the values of m = 10.0 kg, M = 3.0 kg, m_s= 0.20, and m_s= 0.15. Lets first see if the masses will move.
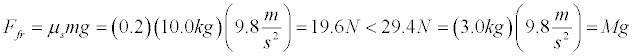Thus, the masses will move and they will have the same acceleration since they are connected. We have pointed the x-coordinate system fo the right for M (the larger horizontal mass) and the y-coordinate system downward for m (the smaller vertical mass). This allows the acceleration to have the same sign for the two masses. We then add the two equations together to eliminate tension and solve for acceleration. There are many other correct ways to do this.
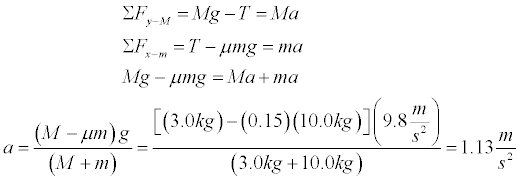
• Let's use the vertical mass to solve for tension.

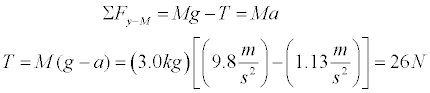
• Experiment with several other values of the masses and try to predict the acceleration and the tension in the rope.
• Worksheet: Determine the value of the unknown variables on your worksheet.