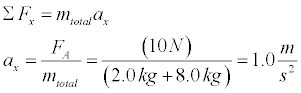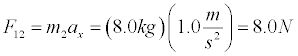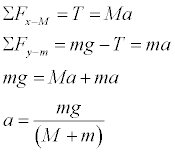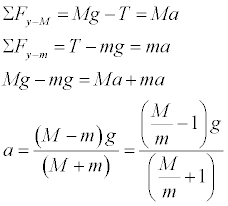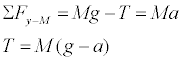Physics 151: Computerized Recitation #4
Forces (Applications of Newton's Second Law)
This excursion will focus on applications of Newton's Second Law where friction is small enough to be ignored. We will focus on problems where two masses interact through either a contact force or by tension since they are connected by a cord.
Simulation 1: Two Masses Being Pushed on a Horizontal Flat Surface
The physlet above allows you to watch a force pushing two boxes across a frictionless horizontal surface for 10 seconds. You may use the pause button to stop the animation and the step buttons to move through the
animation frame by frame. You can click anywere on the grid and read out the x and y values (assume units are in meters) of the cursor location. Click Simulate! below to begin the animation.
Suggestions for Exploration
- Setup the simulation for an applied force of 10 N, mass1 = 2.0 N, and mass 2 = 8.0 N. The acceleration must be:
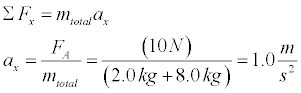
Note that the value obtained for acceleration can be easily checked in this simulation (and all that follow). Since the velocity is zero at time t = 0, the distance traveled in time t is x = (1/2)at2. Simply measure the position x with the cursor at a certain time.
The contact force of mass 1 on mass 2 is the force responsible for the acceleration of mass 2. In the absence of friction there is no other force in the x-direction.
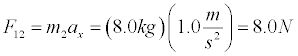
What is the contact force of mass 2 on mass1?
Feedback
- Experiment with several other values of the applied force and the masses and try to predict the acceleration and the contact force.
- Worksheet: Determine the values of the unknown force and masses. Show all calculations and reasoning on your worksheet.
Simulation 2: Horizontal Atwood's Machine
The physlet above allows you to watch two masses connected by a massless rope strong over a massless pulley. One mass moves vertically and pulls the other horizontally. This is commonly referred to as a horizontal Atwood's Machine. The horizontal surface is assumed to be frictionless. Click Simulate! below to begin the animation.
Suggestions for Exploration
- Are there any values of mass for which the masses will not move? Feedback
- Construct free body diagrams for the two masses and verify the following derivation for the acceleration of the masses. We have pointed the x-coordinate system fo the right for M (the larger horizontal mass) and the y-coordinate system downward for m (the smaller vertical mass). This allows the acceleration to have the same sign for the two masses. We then add the two equations together to eliminate tension and solve for acceleration. There are many other correct ways to do this.
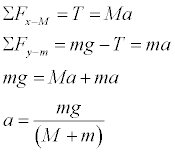
- Since the acceleration of the horizontal mass is entirely caused by the tension in the rope, one can easily solve for tension from T = Ma.
- Experiment with several other values of the masses and try to predict the acceleration and the tension in the rope.
- Worksheet: Determine the value of the unknown masses. Show all calculations and reasoning on your worksheet.
Simulation 3: Atwood's Machine
The physlet above allows you to watch two masses free to move vertically that are connected by a massless rope over a massless frictionless pulley. You are allowed to specify values for the mass ratio -- the value of the mass on the left divided by the value of the mass on the right. Click Simulate! below to begin the animation.
Suggestions for Exploration
- Run the simulation with both masses at 5 kg. Can you explain what happens?
- Construct free body diagrams for the two masses and verify the following derivation for the acceleration of the masses. We have pointed the y-coordinate system downward for M (the larger mass on the left) and upwards for m (the smaller mass on the right). This allows the acceleration to have the same sign for the two masses. (You might at first think that it is not legal to have different coordinate systems for the two masses, but this is equivalent to pointing the two coordinate systems in the same direction and multiplying one of the equations by negative 1. )
We then add the two equations together to eliminate tension and solve for acceleration. There are many other correct ways to think of this.
The mass ratio is included since it is one method of descibing the Atwood's Machine that is found in many textbooks and can make the acceleration formula easier to evaluate.
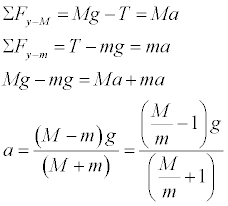
We can use the acceleration to evaluate tension.
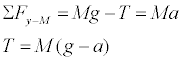
Can you determine a formula for tension using the mass on the right m? Feedback
- Experiment with several other values of the mass ratio and try to predict the acceleration.
- Worksheet: Determine the value of the unknown masses. Show all calculations and reasoning on your worksheet.