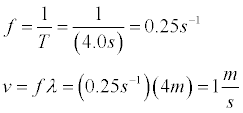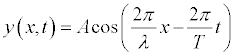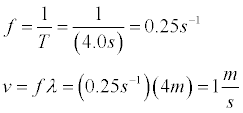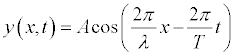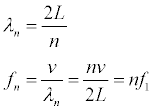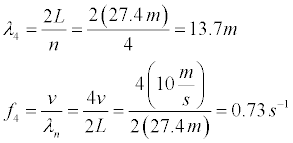Physics 151: Computerized Recitation #10
Wave Motion
This recitation will focus on wave motion and the superposition of waves. Please experiment with the Physlet simulations below and complete the required calculations on your worksheet.
Simulation 1: Parameters of a Traveling Wave
The physlet above displays a traveling harmonic wave. You can control the wavelength, amplitude, and period of the animated wave and the resulting frequency and velocity are then
given.
Suggestions for Exploration
- Set up the simulation for l = 4.0 m, amplitude
= 4.0 m, and period = 4.0 s. The frequency and velocity are then given by:
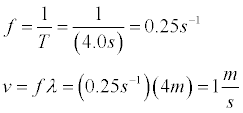
- Experiment with the values of wavelength, amplitude, and period until you
can predict how a parameter change will affect the resulting wave.
- The generic equation for a traveling wave is:
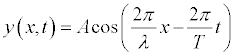
- Worksheet:Determine the equation of the wave
for the l = 4.0 m, amplitude = 4.0 m, and period
= 4.0 s simulation.
- Worksheet:Determine the values of the unknown
variables on your worksheet and show all relevant calculations.
Simulation 2: Superposition of Waves
The physlet above allow you to view the superposition of two traveling harmonic waves. You can control the wavelengths, amplitudes, and velocities of the waves. Giving a wave a negative amplitude is effectively shifting it by half a cycle (or 180°).
Suggestions for Exploration
- Set up the simulation for:
- First Wavelength = 1.0 m, First Amplitude = 1.0 m, First Velocity = -2.0 m/s
- Second Wavelength = 1.0 m, Second Amplitude = 1.0 m, Second Velocity = -2.0 m/s
This simulation has the superposition of identical waves traveling in the same direction. Thus, the two waves interfere constructively at all points in space.
- Set up the simulation for:
- First Wavelength = 1.0 m, First Amplitude = 1.0 m, First Velocity = -2.0 m/s
- Second Wavelength = 1.0 m, Second Amplitude = -1.0 m, Second Velocity = -2.0 m/s
This simulation has the superposition of identical waves traveling in the same direction. Thus, the two waves interfere destructively at all points in space.
- Set up the simulation for:
- First Wavelength = 4.0 m, First Amplitude = 1.0 m, First Velocity = 1.0 m/s
- Second Wavelength = 4.0 m, Second Amplitude = 1.0 m, Second Velocity = -1.0 m/s
This simulation has the superposition of identical waves traveling in opposite directions - which yields a standing wave.
- Set up the simulation for:
- First Wavelength = 1.0 m, First Amplitude = 1.0 m, First Velocity = 1.0 m/s
- Second Wavelength = 4.0 m, Second Amplitude = 4.0 m, Second Velocity = 2.0 m/s
This simulation has the superposition of waves of different frequencies - which yields a beat pattern. The beat frequency is the absolute value of the difference between the two frequencies (0.5 Hz).
Worksheet: Run the simulator for the following combinations of variables and describe the pattern that you see.
| Superposition | 1st λ | 1st Amp | 1st v | 2nd λ | 2nd Amp | 2nd v |
|---|
| #1 | 2 | 1 | 2 | 2 | 1 | -2 |
| #2 | 2 | 1 | 1 | 8 | 1 | -1 |
Simulation 3: Standing Waves on a String
The physlet above displays a standing wave on a string with fixed ends. The string is 27.4 m long and waves travel at a velocity of 10 m/s on the string.
Suggestions for Exploration
- The wavelength and frequency of the standing waves on a string are given by:
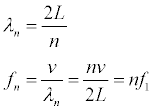
- The wavelength and frequency for the 3rd overtone (4th harmonic) are given by:
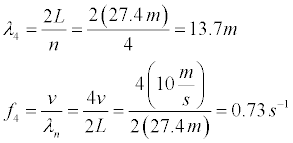
- Worksheet: Determine the wavelength and frequency of the 7th harmonic on your worksheet and show all relevant calculations.
- Worksheet: Determine the unknown harmonic on your worksheet and show all relevant calculations.